中考数学试题研究：什么是奇异四边形？邻等对

在初中平面几何中，除了平行四边形和梯形这两类特殊四边形外，还有一种特殊四边形也是很常见的，那就是邻等对补四边形。

什么是邻等对补四边形呢？所谓邻等对补四边形，是指有一组邻边相等，并且对角互补的四边形，又称等补四边形，或者奇异四边形。

那么，这种邻等对补四边形到底有何特殊之处呢？

首先，它把四点共圆和旋转变换这两大重要的几何解题技法融合在了一种图形中，为解决一些四边形难题，提供了很好的思路和途径。

其次，一些特殊角的邻等对补四边形还具有很多的几何特性，掌握这些性质可以帮助我们快速解决一些选择、填空小题，对于一些特定的几何培优题也可以快速找到突破口！

所以，这种邻等对补四边形非常值得我们去深入研究，下面我们来看下它们具体有哪些性质。

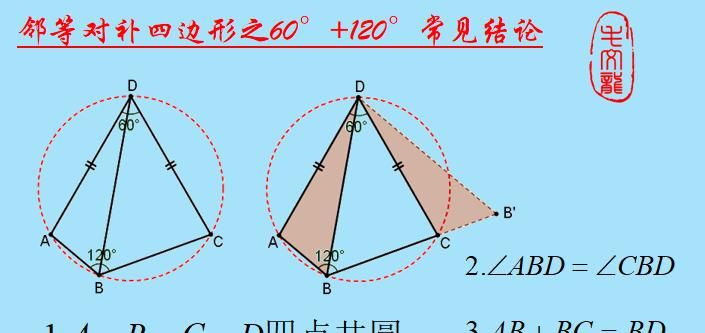
最特殊的邻等对补四边形莫过于这种60°+120°的结构了，它有哪些性质呢？

首先，就是四个顶点共圆，其次，就是对角线BD平分∠ABC，这个结论放在圆中很好证明，等弦对等角即可。最后我们通过旋转变换得到了一个等边三角形，从而得到AB+BC=BD这种线段的数量关系。

前两个结论是邻等对补四边形的通用结论，最后的线段关系，不同的图形有各自的结论。

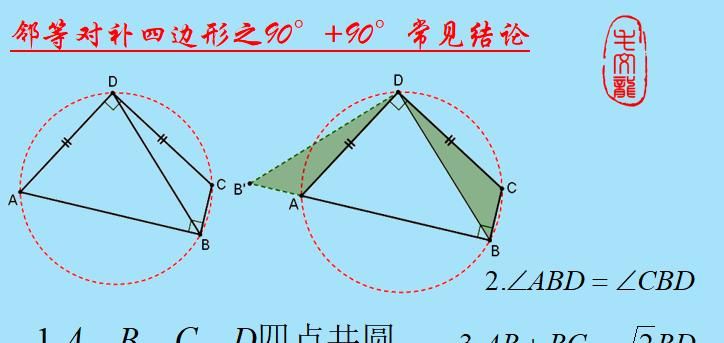
第二种常见的邻等对补四边形就是这种双90°的结构，仍然是通过四点共圆和旋转变换可以证得以上3个结论。

可能出题者更青睐于此这种图形，导致它出现的频率较高，题目类型主要是计算题，一般是求对角线长度和四边形的面积。掌握了上述思想方法和结论后，此类题便可迎刃而解。

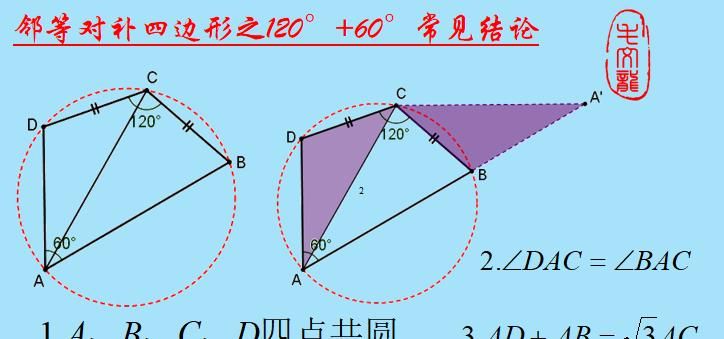
最后一种特殊的邻等对补四边形就是这种120°+60°的结构了，具体结论和证明方法在此不再赘述。

下面我们结合几道具体的例题，来看下此类题的具体考法和邻等对补四边形的性质如何运用。

以上5道例题就是初中邻等对补四边形的常见考法，同学们可以先自己尝试着挑战一下，看看普通的方法这类题怎么处理？接下来再看我下面的解析，相信就可以感受到这些数学思维方法和几何性质结论的妙用了。

例1这道题是很经典的例题，也是一道高频考题，如果我们试图用普通方法进行求解的话，很显然，难度不小。

但是，当我们发现它是邻等对补四边形后，便可以直接进行旋转，将其转化为一个等边三角形，然后，代入等边三角形面积公式求解，直接搞定，没有任何难度，的确很巧妙！

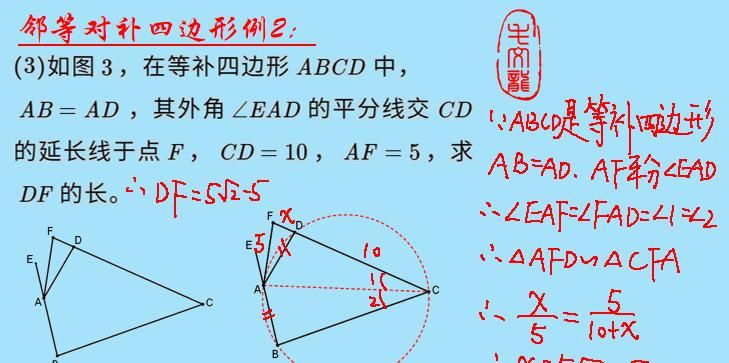
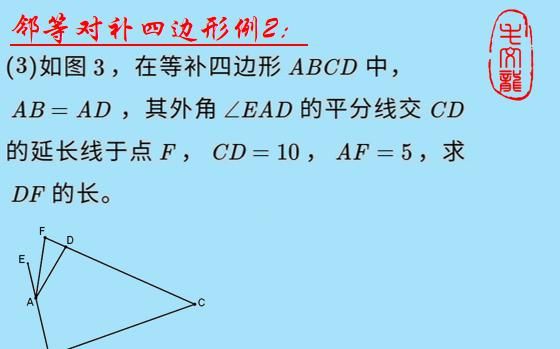
例2这道题，如果直接硬解的话是比较困难的，既然它是邻等对补四边形，那么，我们就可以把隐圆画出来，然后利用圆的相关性质，再结合邻补四边形的性质和相似三角形的知识，此题便可破解。

例3、4是两道填空小题，而且难度还不小，但是，如果我们能够发现图中隐藏的邻补四边形，那么我们就可以直接代入公式进行计算，大大简化了解题步骤，考试时可以节省时间，提高解题效率。

当然，如果这两题还不足以说明问题，下面这道例5完全可以有效证明。请看解答图：

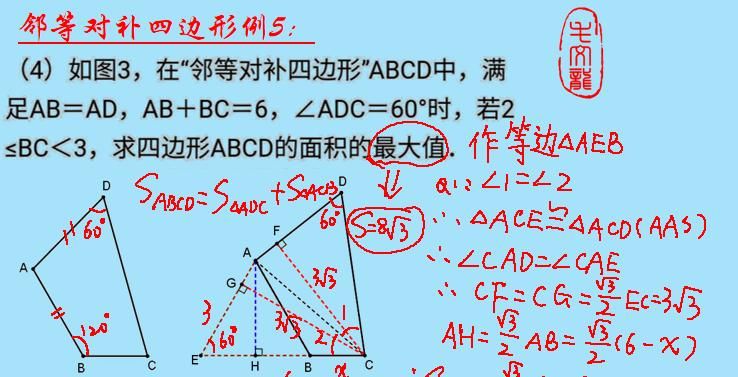
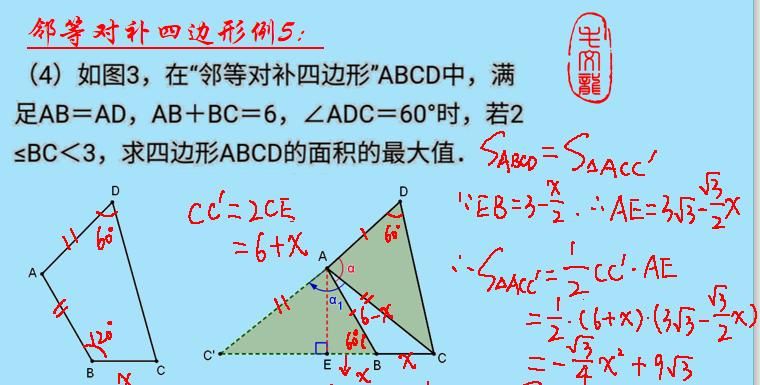
例5这道题难度就很大了，如果按照常规思路可能很难突破，如解答图1，辅助线相对较为复杂，而且即便如此，还是得用到邻等对补四边形的相关结论才可以勉强求解，而如果我们采用第二种解法，通过旋转变换另辟蹊径，此题便会简单很多，极其轻松地就可以破解了。

当然，这种邻等对补四边形的性质还不止于此，这篇文章如果能激起同学们的兴趣，完全可以自己去研究一番，相信在钻研的过程中，一定可以收获更多知识和乐趣。

孩子们，去追寻吧！

文章来源：《试题与研究》 网址: http://www.styyjzz.cn/zonghexinwen/2020/0528/347.html