欧拉、欧几里得、笛卡尔都没能解决的数学题目

萧箫 发自 凹非寺量子位 报道 | 公家号 QbitAI

欧拉、欧几里得、笛卡尔、尼科马修斯都没能解决的千年数学题目，还有破解的可能吗？

还真有可能。

最近，一位名为佩斯·尼尔森（Pace Nielsen）的数学家开辟了一种新方法，给这个“千年困难”提供了别样的解决思路。

这个数学题目是奇数完美猜想，事实上，它的定义非常简单：

是否存在一个奇数，使得它是完美数？

然而，这个“简朴题目”却在证实过程中变得越来越复杂，甚至成了数学上悬而未解的“疑案”。

有“完美”的奇数吗？

首先来解决一个概念：“完美数”是什么？

这个数最早被毕达哥拉斯发现，他给出了完美数的定义：

一个完美数（必需是自然数），假如将它除了自身以外的所有因数相加，即是它自己。

例如，6就是一个完美数。

因为6=1×6=2×3，所以6除了自己以外，它的约数还有1、2、3。

可以看见，这三个约数的和为1+2+3=6，刚好即是6自己。

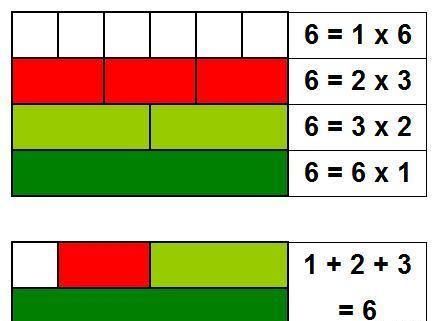
除了6以外，还有28、496、8128……

根据这些排列出来的数，欧几里得设计了一个公式，用来天生完美数。

假设一个质数p，而2 ^ p - 1 （2的p次方-1）也同样是一个质数，那么2^(p-1)×(2^p-1)就会是一个质数。

题目被解决了？

没有。

2000年后，欧拉研究这个题目时发现，欧几里得给出的公式，实际上只能天生完美数中的每个偶数。

数学家尼科马修斯（Nicomachus）下过定论，“完美数只能是偶数”，但没有证实。

也就是说，没人知道完美奇数猜想是否准确——到底存不存在这样的奇数（Odd Perfect Numbers，简称OPN），使得它是完美数？

题目吸引了不少数学家研究，OPN的限制前提也开始被提出：不能被105整除；任何OPN都必需大于10的2000次方……

限制前提越来越多，OPN存在的可能性也在被缩小——像渔夫“收网”一样，越来越多的奇数正在被排除。

根据数学上的定理，假如两个限制前提互相矛盾，那么OPN就不可能存在。

然而，跟着限制前提越来越多，前提之间却没有一点矛盾的迹象，导致这个猜想一直没被证实。

对此，数学家约翰·沃伊特表示：证实一种事物的存在非常简单，但证实它不存在，却要难题得多。

“收网”行不通，尝尝找相似

与众多研究“完美奇数猜想”的数学家一样，尼尔森一开始也试图增加OPN的限制前提，以证实它不存在。

但他发现，这样的证实方法会跟着限制前提的增加变得十分复杂。

为此，尼尔森研究前人的成果，发现了笛卡尔留下的“欺骗数”（spoof number）。

事实上，这是笛卡尔试图证实“完美奇数”存在的一个失败案例：他假装某些数是质数，以此得出了一个假冒版的“完美奇数”。

例如，198585576189是一个巨大的数，而22021是它的一个因数。

笛卡尔在证实过程中，假装22021是质数，将它和198585576189的其他因数相加，就即是198585576189自己，符合“完美奇数”的定义。

实在，22021即是19×19×61，这个数也因此成为了一个“欺骗数”。

此外，后人还在笛卡尔研究的基础上，弄了一个“恶搞版”欺骗数——他假设负数也能成为完美数（完美数只能是自然数），证实了22017975903是所有因数的和。

但假如将这种“欺骗数”用来证实“完美奇数”不存在呢？

尼尔森与研究团队用了几年时间，找出了所有的“欺骗数”，并开始研究这些欺骗数的特点。

他提出了自己的观点：“完美奇数”应该具有“欺骗数”的一切特性，而且还自带特殊前提。

而假如能证实“欺骗数”不符合“完美奇数”的任何一个限制前提，那么“完美奇数”就不可能存在。

简朴来说，因为“完美奇数”不能被105整除，那么假如“欺骗数”都可以被105整除，“完美奇数”就不存在。

固然团队还没有找到这样的限制前提，但这无异于给“证实不可能”提供了一个更好的思路。

约翰·沃伊特表示，这是个伟大的尝试。

也有网友表示，这离困难的解决又近了一点。

尼尔森与奇数完美猜想

尼尔森第一次与完美数猜想结缘，是在高中数学竞赛上。

文章来源：《试题与研究》 网址: http://www.styyjzz.cn/zonghexinwen/2020/1001/700.html